Docking and MDS: Introduction

The synthesis of piperamides involves a complex metabolic pathway that requires specific enzymatic reactions. Identifying enzymes capable of efficiently catalyzing these reactions is crucial for optimizing the metabolic pathway design. Utilizing the methodology described in the "Alternative Enzyme Selection" section, we obtained a pool of enzymes and synthesized the coding sequences (CDS) for 126 candidates, excluding 13 due to their large size. Our objective is to experimentally assess their enzymatic activities in the future, using molecules that could serve as substrates for the proposed reactions within the piperamide synthesis pathway.

To prioritize enzymes for experimental validation, we conducted a molecular docking-based screening of 121 enzymes corresponding to the three key reactions of interest. Additionally, we included three enzymes hypothesized to catalyze the same reactions in black pepper plants, based on differential expression analysis and previous docking studies (see "Differential Expression Analysis" and "Docking 1" sections). Molecular docking estimates the binding energy between an enzyme and a ligand, facilitating the identification of enzymes with high affinity and specificity for particular ligands. It is, therefore, an essential tool for selecting enzymes that may enhance metabolic efficiency in a metabolic pathway.

However, conventional docking approaches often assume rigidity in molecular structures, neglecting the conformational flexibility inherent in both enzymes and ligands. Biological molecules are dynamic entities capable of adopting multiple conformations, which significantly influence their interactions and binding affinities. Recognizing this limitation, we pursued a more comprehensive analysis of the enzymes exhibiting the strongest binding affinities from the docking results.

After evaluating the binding affinity data, we selected 12 enzymes from Group 5 that demonstrated the highest affinities for their respective ligands. These enzymes were subjected to molecular dynamics (MD) simulations using GROMACS 2024.1 to further investigate enzyme-ligand interactions. MD simulations account for molecular flexibility, solvent effects, and dynamic conformational changes, providing a more realistic and detailed representation of the system. This approach is essential for validating and refining initial docking predictions, ensuring that the selected enzymes are indeed capable of effectively interacting with specific ligands within the context of our metabolic pathway design.

Molecular Docking

A molecular docking analysis was performed to identify the enzymes with the highest affinity and specificity for the target ligands. The process was fully automated within a Jupyter notebook (Figure 1), utilizing the following tools: UCSF Chimera 1.18, OpenBabel 3.1.1, AutoDockTools (MGLTools 1.5.7), AutoDock Vina v1.2.3, Python 2.7, Python 3.10, and PyMOL. The docking workflow is shown in Figure 1, and the details of each procedure are as follows

Figure 1: Analysis workflow with docking, automated through a Jupyter notebook and using parallelization to accelerate computation.

Protein preparationProtein structures in PDB format were converted to MOL2 format using UCSF Chimera 1.18. During this process, the following steps were performed:

To ensure the integrity and quality of the molecular structures, OpenBabel was used to validate the MOL2 files. The validated MOL2 files were then converted to PDBQT format using the prepare_receptor4.py script (version 1.11) from AutoDockTools.

Ligand and Cofactor PreparationFor all cases, the ligand or cofactor of interest was obtained from the files described in the Docking 1 section for reactions 5, 6, and 10. The 3D structure of each ligand was minimized using UCSF Chimera. Subsequently, the prepare_ligand4.py script (version 1.5.4.1) from AutoDockTools was used to convert and prepare the ligands in PDBQT format.

Docking Configuration and ExecutionA configuration file (config.txt) was created with specific parameters for the docking simulations. The search box was centered at coordinates (1, 1, 1) and assigned a size of 80 × 80 × 80 Å, encompassing the entire active site of the enzymes. Additionally, the exhaustiveness parameter was set to 32 to obtain more accurate results compared to the default value of 8. AutoDock Vina was then used to perform molecular docking between the selected enzymes for each reaction and the corresponding ligand.

To optimize processing time, parallel execution was implemented using Python’s multiprocessing module, running 20 processes simultaneously to match the number of available CPU cores.

Molecular Dynamics Simulation

To evaluate the structural stability and dynamic interactions between the selected enzymes and their ligands, molecular dynamics (MD) simulations were performed using GROMACS 2024.1. This process involved detailed preparation of proteins and ligands, system setup, simulation execution, and subsequent analysis of the results.

Figure 1: Analysis workflow with docking, automated through a Jupyter notebook and using parallelization to accelerate computation.

Protein preparationTwelve enzymes from group 5, which exhibited the best binding affinities with ferulic acid in the docking analysis, were selected for MD simulations. The three-dimensional structures of these proteins were obtained from the Protein Data Bank (PDB) or generated via homology modeling using tools like AlphaFold2 when experimental structures were not available.

Crystallographic water molecules, irrelevant ligands, missing residues, and structural inconsistencies were all addressed using UCSF Chimera 1.18. Additionally, appropriate protonation states for amino acid residues were assigned in Chimera, assuming a physiological pH of 7.4. Missing hydrogen atoms were added using either UCSF Chimera or the pdb2gmx module of GROMACS, depending on the workflow requirements. For force field selection, the AMBER99SB-ILDN force field was chosen, as it is well-suited for accurately simulating protein dynamics.

To ensure the integrity and quality of the molecular structures, OpenBabel was used to validate the MOL2 files. The validated MOL2 files were then converted to PDBQT format using the prepare_receptor4.py script (version 1.11) from AutoDockTools.

Ligand and Cofactor PreparationThe files for ligands of interest—ferulic acid, 3,4-methylenedioxycinnamic acid, and piperidine—were downloaded from SwissParam.

SolvationEach complex was placed in a dodecahedral simulation box, maintaining a minimum distance of 1.0 nm between the complex and the box edges. The TIP3P water model was used for explicit solvation. Sodium (Na⁺) or chloride (Cl⁻) ions were added to neutralize the system, and the ionic concentration was adjusted to 0.15 M to simulate physiological conditions.

To optimize processing time, parallel execution was implemented using Python’s multiprocessing module, running 20 processes simultaneously to match the number of available CPU cores.

Topology File Generation:The complete topology file (topol.top) was generated using the gmx pdb2gmx module of GROMACS.

Energy MinimizationThe energy minimization of the system was performed using the steepest descent algorithm (integrator = steep). The minimization was set to stop when the maximum force on any atom was less than 1000.0 kJ/mol (emtol = 1000.0), with an energy step size of 0.01 (emstep = 0.01). A maximum of 50,000 steps (nsteps = 50,000) was allowed for the minimization process.

Neighbor searching was updated every step (nstlist = 1) using a grid-based method (ns_type = grid) with a cutoff distance of 1.2 nm (rlist = 1.2). Electrostatic interactions were handled using the Particle Mesh Ewald method (coulombtype = PME) with a cutoff for long-range electrostatics set to 1.2 nm (rcoulomb = 1.2). Van der Waals interactions were computed using a force-switch modifier (vdw-modifier = force-switch), with a switch distance of 1.0 nm (rvdw-switch = 1.0) and a cutoff at 1.2 nm (rvdw = 1.2). Periodic boundary conditions were applied in all directions (pbc = xyz), and dispersion corrections were not applied (DispCorr = no).

NVT EquilibrationThe NVT equilibration of the protein-cofactor-ligand complex was conducted using the leap-frog integrator (integrator = md) for a total of 1,000 ps (nsteps = 500000, dt = 0.002 ps), with position restraints applied to the protein, cofactor, and ligand (define = -DPOSRES). Energies, log files, and coordinates were saved every 1 ps (nstenergy = 500, nstlog = 500, nstxout-compressed = 500).

This was the first dynamics run (continuation = no), and the LINCS algorithm was used to constrain all bonds involving hydrogen atoms (constraint_algorithm = lincs, constraints = h-bonds) with a single iteration (lincs_iter = 1) and a fourth-order expansion (lincs_order = 4) for accuracy. Neighbor searching was performed with the Verlet cutoff scheme (cutoff-scheme = Verlet), with van der Waals interactions handled using a force-switch modifier (vdw-modifier = force-switch), and a short-range cutoff of 1.2 nm (rvdw = 1.2). Electrostatic interactions were treated with the Particle Mesh Ewald method (coulombtype = PME), with a short-range cutoff of 1.2 nm (rcoulomb = 1.2) and a Fourier grid spacing of 0.16 nm (fourierspacing = 0.16).

Temperature coupling was achieved using a V-rescale thermostat (tcoupl = V-rescale), with separate coupling groups for the protein-cofactor-ligand complex and the solvent (tc-grps = Protein_Cofactor_Ligand Water_and_ions), maintaining a reference temperature of 300 K for both groups (ref_t = 300 300) and a time constant of 0.1 ps (tau_t = 0.1 0.1). No pressure coupling was applied during the NVT phase (pcoupl = no). Periodic boundary conditions were applied in all three dimensions (pbc = xyz).

Initial velocities were generated from a Maxwell distribution at 300 K (gen_vel = yes, gen_temp = 300) with a randomly generated seed (gen_seed = -1). Dispersion corrections were not applied for proteins using the C36 additive force field (DispCorr = no).

NPT EquilibrationThe NPT equilibration of the protein-cofactor-ligand complex was performed using the leap-frog integrator (integrator = md) for a total of 1,000 ps (nsteps = 500000, dt = 0.002 ps), with position restraints applied to the protein, cofactor, and ligand (define = -DPOSRES). Energies, log files, and coordinates were saved every 1 ps (nstenergy = 500, nstlog = 500, nstxout-compressed = 500).

This simulation continued from the NVT equilibration phase (continuation = yes), using the LINCS algorithm to constrain bonds involving hydrogen atoms (constraint_algorithm = lincs, constraints = h-bonds), with one iteration (lincs_iter = 1) and a fourth-order expansion (lincs_order = 4) for accurate bond handling. Neighbor searching was carried out using the Verlet scheme (cutoff-scheme = Verlet) with a grid-based method (ns_type = grid), a short- range van der Waals cutoff of 1.2 nm (rvdw = 1.2), and a force-switch modifier (vdw-modifier = force-switch).

Electrostatic interactions were calculated using the Particle Mesh Ewald (PME) method (coulombtype = PME), with a cutoff of 1.2 nm for short-range interactions (rcoulomb = 1.2), cubic interpolation (pme_order = 4), and a Fourier grid spacing of 0.16 nm (fourierspacing = 0.16).

Temperature coupling was applied with a V-rescale thermostat (tcoupl = V-rescale) for two groups: the protein- cofactor-ligand complex and the solvent (tc-grps = Protein_Cofactor_Ligand Water_and_ions), maintaining a reference temperature of 300 K for both (ref_t = 300 300) with a time constant of 0.1 ps (tau_t = 0.1 0.1).

Pressure coupling was performed using the Parrinello-Rahman barostat (pcoupl = Parrinello-Rahman) with isotropic scaling (pcoupltype = isotropic), a time constant of 2.0 ps (tau_p = 2.0), and a reference pressure of 1.0 bar (ref_p = 1.0). The isothermal compressibility of water was set to 4.5 × 10⁻⁵ bar⁻¹ (compressibility = 4.5e-5), and reference coordinate scaling was applied to the center of mass (refcoord_scaling = com).

Periodic boundary conditions were used in all three dimensions (pbc = xyz). Dispersion corrections were not applied for proteins using the C36 additive force field (DispCorr = no), and velocity generation was turned off (gen_vel = no) after the NVT equilibration phase.

Production Molecular Dynamics SimulationsThe molecular dynamics (MD) simulation of the protein-cofactor-ligand complex was performed using the leap- frog integrator (integrator = md) for a total of 10 ns (nsteps = 5000000, dt = 0.002 ps). Energies, log updates, and coordinates were recorded every 10 ps (nstenergy = 5000, nstlog = 5000, nstxout-compressed = 5000).

The simulation continued from the NPT equilibration phase (continuation = yes), with all bonds involving hydrogen constrained using the LINCS algorithm (constraint_algorithm = lincs, constraints = h-bonds), employing one iteration (lincs_iter = 1) and a fourth-order expansion (lincs_order = 4) to ensure accuracy.

Neighbor searching was performed using a Verlet cutoff scheme (cutoff-scheme = Verlet), with a grid-based search method (ns_type = grid). The cutoff for short-range interactions was set to 1.2 nm for both van der Waals (rvdw = 1.2) and electrostatic interactions (rcoulomb = 1.2), with van der Waals forces being treated with a force- switch modifier (vdw-modifier = force-switch). Long-range electrostatics were calculated using the Particle Mesh Ewald (PME) method with cubic interpolation (pme_order = 4) and a Fourier grid spacing of 0.16 nm (fourierspacing = 0.16).

Temperature coupling was achieved using the V-rescale thermostat (tcoupl = V-rescale), with separate coupling groups for the protein-cofactor-ligand complex and the solvent (tc-grps = Protein_Cofactor_Ligand Water_and_ions), maintaining a reference temperature of 300 K for both groups (ref_t = 300 300) and a time constant of 0.1 ps (tau_t = 0.1 0.1).

Pressure coupling was performed using the Parrinello-Rahman barostat (pcoupl = Parrinello-Rahman) with isotropic scaling (pcoupltype = isotropic), a time constant of 2.0 ps (tau_p = 2.0), and a reference pressure of 1.0 bar (ref_p = 1.0). The isothermal compressibility of water was set to 4.5 × 10⁻⁵ bar⁻¹ (compressibility = 4.5e-5), and reference coordinate scaling was applied to the center of mass (refcoord_scaling = com).

MDS analisysAn automated Python script was used to process and analyze molecular dynamics (MD) simulation data of the protein-cofactor-ligand complex. The script managed multiple simulation datasets, performing essential post- simulation analyses with GROMACS. The required input files for each system, including MD.tpr, MD.xtc, MD.edr, and index.ndx, were verified before analysis.

The analysis steps included recentering and correcting the simulation trajectories, extracting the initial frame (t = 0 ns), calculating the root mean square deviation (RMSD) of the ligand relative to the protein, and computing the RMSD of the protein backbone and the root mean square fluctuation (RMSF) of the protein. Hydrogen bonds between the ligand and protein were identified, and the radius of gyration and total energy of the system were calculated. The resulting data were saved as .xvg files in their respective analysis directories.

For comparative analysis across different systems, data were extracted from the .xvg files, and plots were generated for RMSD, RMSF, radius of gyration, hydrogen bonds, and energy. All comparison plots were stored in a designated directory for further interpretation. Python’s matplotlib and pandas libraries were used for data visualization and handling.

Results

The binding affinities obtained from the protein groups for each reaction through molecular docking were visualized using density plots, illustrating the distribution of binding affinities for each group. The position of the enzymes that we initially proposed to catalyze the reactions is highlighted with a red line (Figure 2).

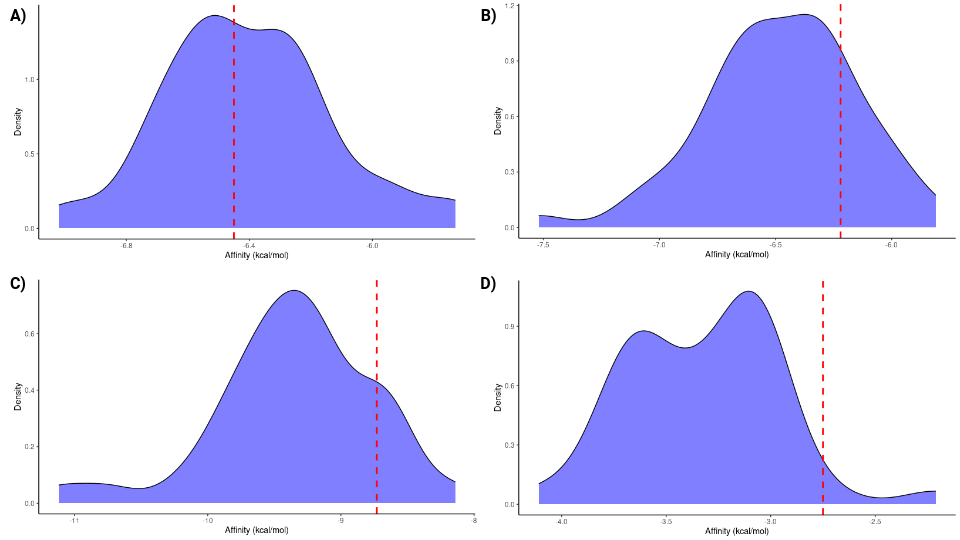
Density plots of ligand binding affinities

Figure 2: Density plots of ligand binding affinities obtained from docking simulations. The red line indicates the position of the enzyme we initially proposed for each reaction. (A) Group 5 enzymes and their ligand. (B) Group 5 enzymes with their cofactor and ligand. (C) Group 6 enzymes and their ligand. (D) Group 10 enzymes and their ligand.

To assess the impact of the cofactor on the ligand binding affinity to group 5 proteins, we compared the binding affinities obtained under two conditions: with and without the cofactor. When considering the average binding affinity across all enzymes, the presence of the cofactor did not significantly affect the overall binding affinity. However, individual proteins exhibited varying responses. The results are presented in a violin plot (Figure 4).

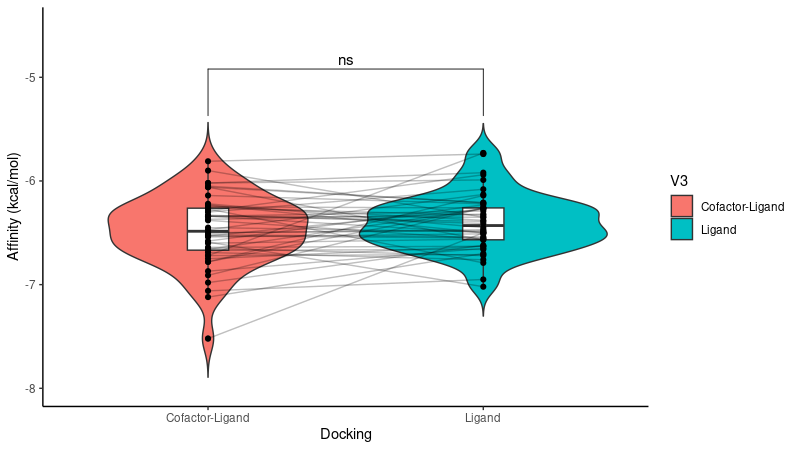
Violin plot comparing binding affinities with and without cofactor

Figure 3: Violin plot comparing ligand binding affinities of group 5 enzymes with and without the cofactor. The plot shows that the difference in total binding affinity of the enzymes with and without the cofactor is not significantly different

Molecular Dynamics Simulation

In the subsequent analysis and filtering step involving molecular dynamics simulations, we randomly selected 7 enzymes from the top 15 with the best binding affinities within group 5 enzymes, all of which were bound to their cofactor.

We analyzed and plotted the ligand-protein RMSD (Figure 4), the RMSF for each protein (Figure 5), the protein backbone RMSD (Figure 6), the number of hydrogen bonds between the ligand and proteins (Figure 7), the radius of gyration for each protein (Figure 8), and the total energy of the protein-ligand systems (Figure 9).

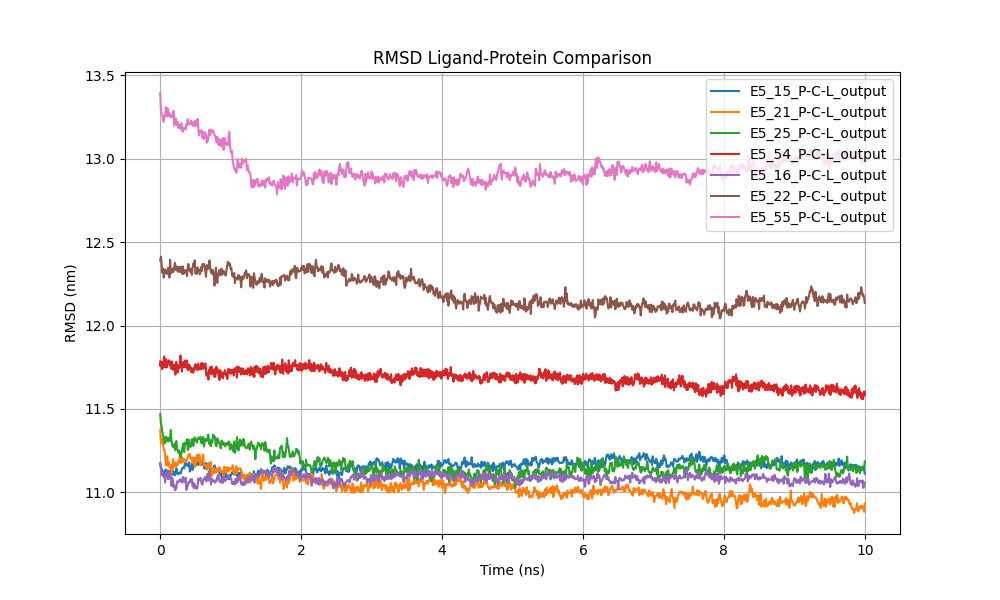
Comparison of ligand-protein RMSD

Figure 4: Comparison of ligand-protein RMSD, representing the deviation of the ligand's atomic positions relative to the protein over time.

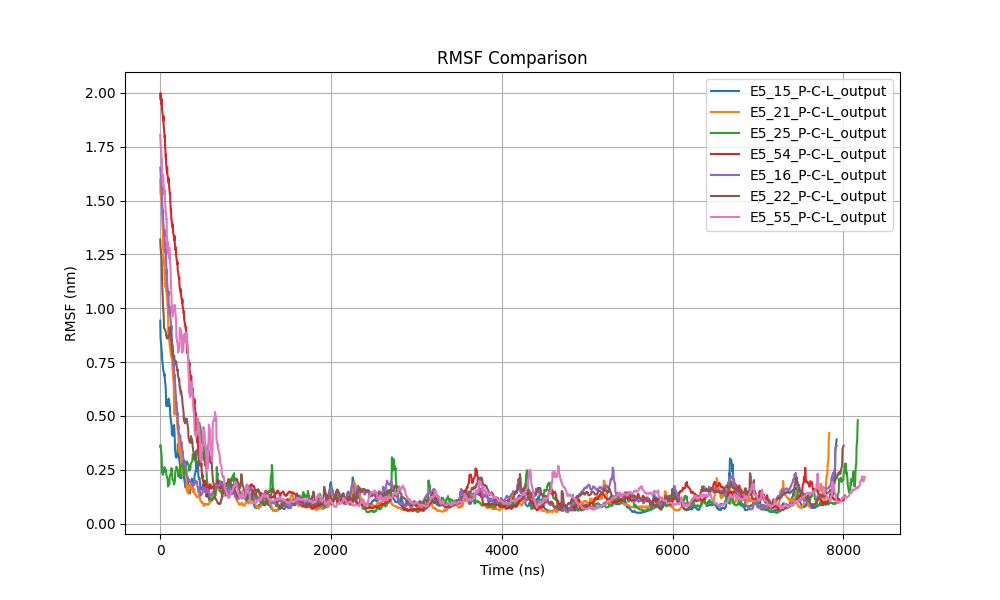
RMSF comparison

Figure 5: Comparison of RMSF for each protein, highlighting regions of flexibility or stability.

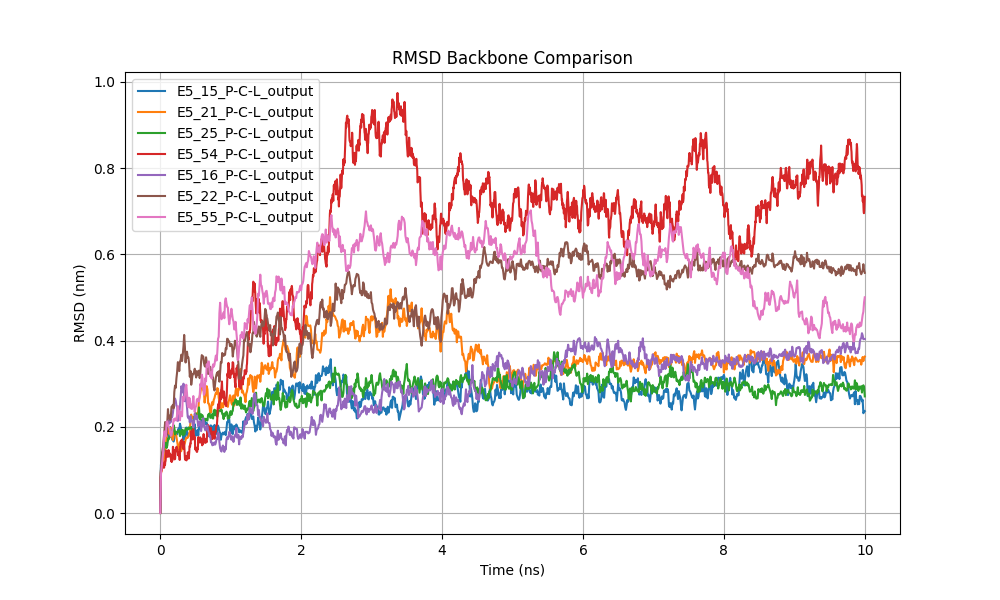
Protein backbone RMSD

Figure 6: Protein backbone RMSD comparison showing structural stability.

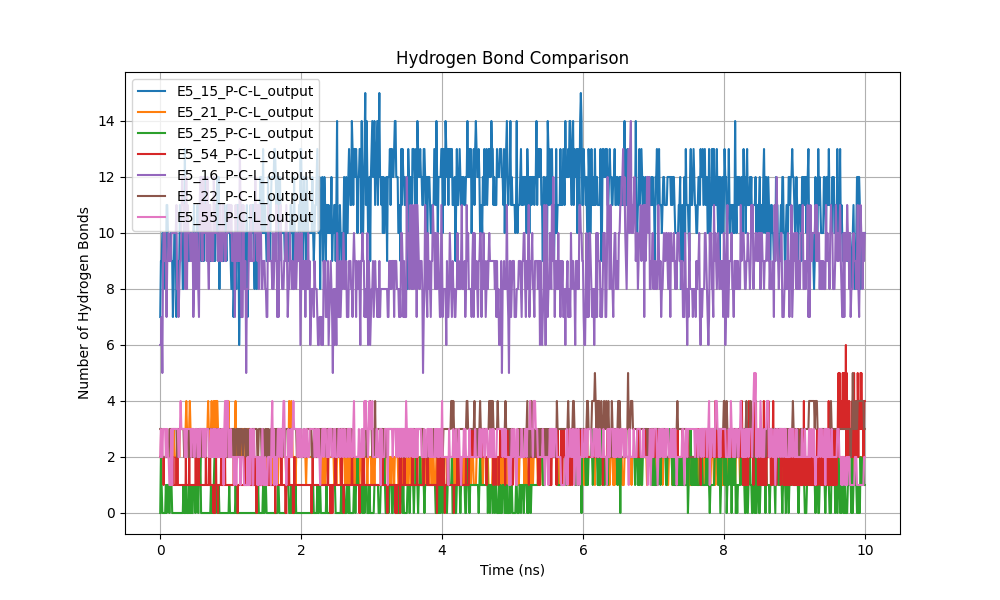
Hydrogen bonds comparison

Figure 7: Comparison of the number of hydrogen bonds between the ligand and protein.

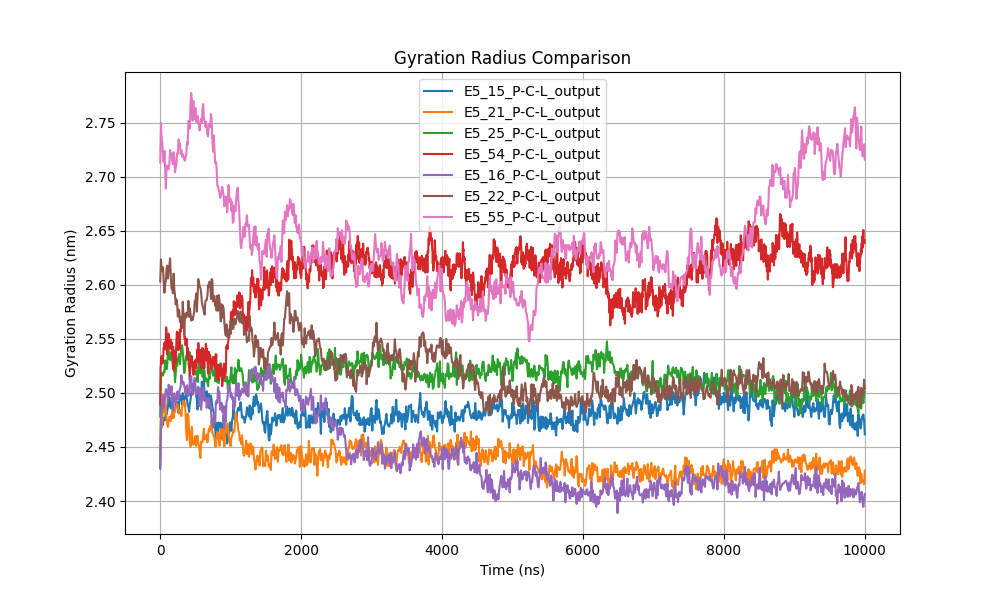
Radius of gyration comparison

Figure 8: Radius of gyration comparison, indicating changes in protein compactness.

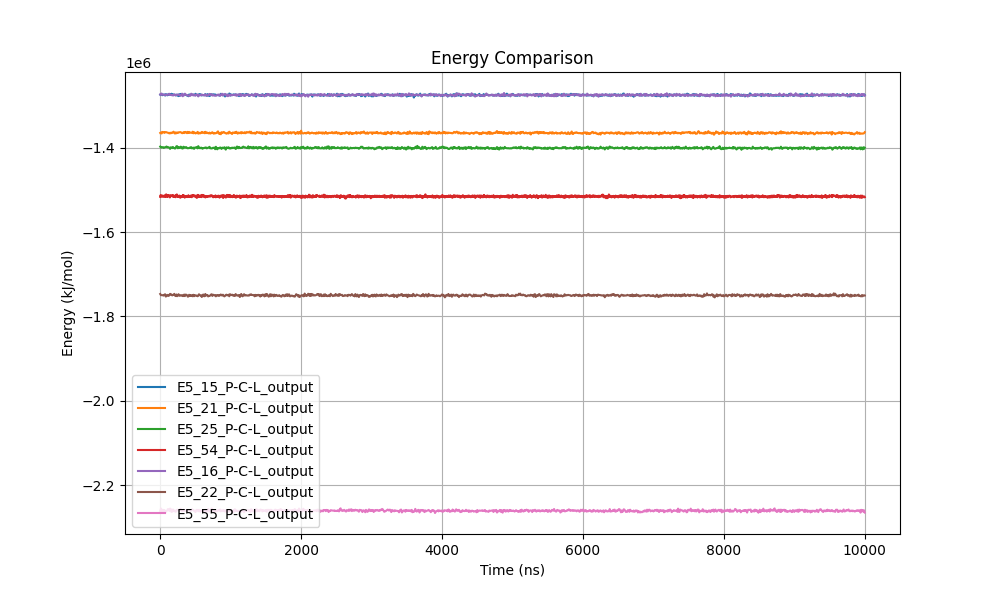
Total energy comparison

Figure 9: Comparison of total energy of the protein-ligand systems.

Discussion

This study combines molecular docking and molecular dynamics (MD) simulations to explore critical enzyme-ligand interactions relevant to the design of the metabolic pathway for piperamide synthesis. By integrating these computational approaches, our goal was to identify and characterize enzymes capable of catalyzing specific reactions to optimize metabolic efficiency.

Molecular Docking Analysis

The density and violin plots (Figures 3 and 4) indicated that, for Group 5 enzymes, the presence of cofactors did not significantly alter ligand binding affinities when considering the average across all enzymes in this group. However, individual enzyme responses varied, suggesting that cofactors may have a crucial impact in specific cases.

This variability underscores the importance of examining cofactor-enzyme interactions on an individual basis, as they can significantly influence enzymatic specificity and activity. These nuances, not always apparent in static docking analyses, highlight the necessity for dynamic studies to fully understand these interactions and their effects on the stability and functionality of enzyme-ligand complexes.

Molecular Dynamics Simulations

The subsequent MD simulations provided a more refined and dynamic analysis of enzyme-ligand interactions, accounting for the flexibility of both proteins and ligands in a simulated physiological environment. MD is essential for capturing the temporal evolution of molecular complexes, allowing for validation and refinement of the initial docking predictions.

Ligand RMSD Analysis

In comparing the RMSD (Root Mean Square Deviation) values of the ligands in six different proteins, patterns emerged indicating variations in ligand-protein interactions, although all systems eventually achieved stable behavior (Figure 5). Differences in RMSD among the proteins suggest that, in some cases—such as systems E5_22 and E5_55—the ligands experienced significant initial displacements. This suggests they may have relocated within the binding site, after which they remained stable for the remainder of the simulation. In these cases, the RMSD decreased markedly at the beginning of the simulation, supporting the hypothesis of early ligand readjustment.

In systems like E5_21, E5_25, and E5_54, the RMSD showed minimal variability from the start, remaining within a constant range close to 1.1 nm. This stability suggests that the ligands in these complexes did not undergosignificant displacements, reinforcing the notion of a firm and sustained interaction from the outset.

Conversely, system E5_16 exhibited a higher RMSD (~1.3 nm) throughout the simulation, stabilizing after a brief initial adjustment phase. This behavior implies that, although the ligand may be positioned further from the binding site compared to other systems, the ligand-protein complex still maintains considerable conformational stability, indicating a stable interaction with a different spatial conformation.

Overall, the observed RMSD stability suggests that, despite initial differences in ligand positioning, the ligand- protein complexes in the six analyzed systems reached a conformationally stable state during the simulation. This indicates enduring interactions between ligands and proteins, with minimal fluctuations once dynamic equilibrium was achieved. The results reinforce the robustness of ligand-protein interactions in these complexes and highlight their potential for biochemical applications, despite variations in initial ligand behaviors.

RMSF Analysis

The comparison of RMSF (Root Mean Square Fluctuation) values for the six proteins, visualized in the combined graph (Figure 5), revealed consistent dynamic patterns across all systems. In each case, a pronounced decrease in RMSF was observed during the first 1,000 ps (1 ns) of the simulation, indicating a significant reduction in initial structural fluctuations. This behavior suggests a common equilibration phase among all proteins, where initial fluctuations due to structural perturbations or adjustment to the simulation environment were rapidly corrected.

After this initial adjustment, RMSF values stabilized at low levels, with fluctuations generally below 0.25 nm, suggesting that the proteins reached a thermally stable state. The uniformity of this behavior implies that the proteins shared similar structural dynamics, with central regions likely remaining rigid and structurally conserved, while larger fluctuations, albeit minor, were concentrated at the chain termini or more flexible regions such as surface loops.

The absence of significant deviations in RMSF during the remainder of the simulation reinforces the idea that the proteins achieved a conformationally favorable and stable state, exhibiting minimal global structural flexibility. Minor variations observed towards the end of the simulation in some proteins, like E5_55, may be due to localized movements in less structured or more exposed regions, without significantly affecting the overall stability of the complex. These results underscore the shared thermal and conformational stability among the simulated proteins.

Protein backbone RMSD

To assess the conformational stability of the three-dimensional models of the tested enzymes, we analyzed the backbone RMSD (Figure 6). The analysis revealed that most proteins achieved structural stability within the first 2 ns of the simulation, with RMSD fluctuations remaining below 0.6 nm in most cases. Proteins E5_15, E5_21, E5_25, and E5_54 exhibited notable stability, maintaining a consistent range of 0.2 to 0.4 nm throughout the simulation, indicating that their folded structures remained consistently stable.

However, some proteins, such as E5_16, displayed more significant fluctuations, with RMSD values peaking near 1.0 nm around nanosecond 6. While these variations indicate greater flexibility in the backbone conformation, thesystem appears to stabilize toward the end of the simulation, suggesting that the overall structure remains stable despite intermediate fluctuations

Similarly, system E5_22 experienced an increase in RMSD, reaching up to 0.8 nm, which could be related to possible conformational adjustments or increased flexibility in specific protein regions.

Hydrogen Bond Analysis

The number of hydrogen bonds between the ligand and protein was identified as an indicator of interaction strength and stability (Figure 7). A higher number of hydrogen bonds generally correlates with stronger binding affinities. Fluctuations in hydrogen bonding patterns reflect the dynamic nature of molecular interactions within the simulation environment.

Comparing the hydrogen bonds formed between the ligand and the simulated proteins revealed notable differences in the stability of these interactions over the 10 ns simulation (Figure X). Systems E5_15 and E5_16 exhibited the highest number of hydrogen bonds, ranging between 10 and 14. This high frequency suggests a stable and consistent interaction between the ligand and the binding site of these proteins. The observed stability reinforces the hypothesis that these complexes are robust and conformationally stable, potentially associated with higher ligand affinity.

In contrast, systems E5_25, E5_21, and E5_22 presented a significantly lower number of hydrogen bonds, varying between 0 and 4 throughout the simulation. This suggests that the ligand may be interacting more transiently or weakly with these proteins, implying lower stability of the ligand-protein complex.

The temporal behavior of hydrogen bonds provided additional insights into complex dynamics. In systems E5_15 and E5_16, hydrogen bonds remained stable with minor fluctuations, indicating that the system reached a steady state early in the simulation. Conversely, in system E5_54, although the number of hydrogen bonds fluctuated between 8 and 12, it remained within a range indicating a relatively strong interaction.

Systems with fewer hydrogen bonds, such as E5_25 and E5_55, showed greater variability toward the end of the simulation, which could indicate a decrease in ligand affinity or rearrangement within the binding site. These fluctuations suggest that the ligand may be losing stability, affecting its ability to consistently remain bound.

Radius of Gyration

The radius of gyration (Figure 8) was utilized to evaluate changes in the compactness of protein structures during the simulation. The data indicate that most proteins maintained a relatively stable radius of gyration, with minor fluctuations, suggesting no drastic changes in structural compactness. Systems E5_15, E5_21, and E5_25 exhibited values between 2.40 and 2.50 nm, implying a compact and stable conformation throughout the simulation without significant expansion or contraction.

Conversely, proteins E5_16 and E5_55 displayed greater variability, with values oscillating between 2.55 and 2.75 nm. This increased variation could indicate fluctuations in protein compactness, suggesting possible structural expansion or flexibility. Specifically, system E5_16 showed a gradual increase in radius of gyration toward the end of the simulation, potentially related to progressive conformational readjustment or structural expansion.

System E5_22 also exhibited significant fluctuations, with values varying between 2.55 and 2.65 nm. These fluctuations could indicate lower structural stability compared to other proteins, potentially affecting functionality or ligand interaction.

Total System Energy

The total energy profiles of the enzyme-ligand complexes were monitored as a general indicator of stability throughout the simulations (Figure 9). The remarkably stable energy lines observed for all systems suggest that the complexes reached equilibrium early and maintained stability during the 10 ns simulation.

Systems E5_16 and E5_55 exhibited the lowest energy values, around -2.2 × 10⁶ kJ/mol, indicating lower potential energy and possibly greater stability compared to other systems. In contrast, systems E5_15, E5_21, and E5_25 showed higher energy values (around -1.4 × 10⁶ kJ/mol), though their profiles remained stable throughout the simulation.

This stability in total energy values suggests an absence of significant fluctuations or indications of structural instabilities or unfavorable interactions in any of the enzyme-ligand complexes. The lack of substantial energy variations reinforces the notion that all systems reached a state of dynamic equilibrium and that ligand-enzyme interactions were favorable. This is a strong indicator that the studied complexes maintained structural and energetic integrity throughout the simulation.

Conclusion

The primary objective of this study was to identify enzymes capable of catalyzing specific reactions essential for the design of a metabolic pathway for piperamide synthesis. By integrating molecular docking and molecular dynamics (MD) simulations, we aimed to select and characterize enzymes that could efficiently facilitate these reactions, thereby optimizing the metabolic pathway.

Starting with a pool of 121 enzymes obtained through alternative selection methods, we performed molecular docking to estimate their binding affinities with target ligands relevant to piperamide synthesis. The docking analysis highlighted 12 enzymes from Group 5 that exhibited the strongest binding affinities, positioning them as promising candidates for further investigation.

Acknowledging the limitations of docking—particularly its assumption of rigid molecular structures and neglect of conformational flexibility—we advanced our analysis by conducting MD simulations using GROMACS 2024.1. This allowed us to delve deeper into the dynamic interactions between the selected enzymes and ligands, accounting for molecular flexibility, solvent effects, and conformational changes over time.

Our MD simulations revealed that while the presence of cofactors did not significantly affect the average binding affinities across Group 5 enzymes, individual enzymes showed varied responses. This underscores the importance of examining cofactor interactions on a case-by-case basis, as they can critically influence enzymatic specificity and activity—factors paramount to the successful design of a metabolic pathway.

The dynamic analyses demonstrated that the enzyme-ligand complexes achieved conformational stability throughout the simulations, as evidenced by stable RMSD and RMSF values, consistent hydrogen bonding patterns, and steady total energy profiles. These findings confirm the robustness of the interactions and the structural integrity of the complexes, suggesting that the identified enzymes are indeed capable of effectively interacting with the specific ligands involved in piperamide synthesis.

By integrating molecular docking with MD simulations, we validated and refined our initial enzyme selections, ensuring they are suitable for incorporation into the metabolic pathway design. This comprehensive approach not only allowed us to efficiently screen and evaluate potential enzyme candidates but also provided detailed insights into their dynamic behaviors and interactions at the molecular level.

Future Directions: Moving forward, experimental validation of these computational predictions is crucial. Confirming the enzymatic activities and interactions observed in silico through biochemical assays and kinetic studies will solidify the potential of these enzymes in practical applications. Successful integration of these enzymes into the metabolic pathway could significantly enhance the viability of piperamide synthesis, contributing to advancements in synthetic biology and metabolic engineering.

In Conclusion, this study demonstrates the effectiveness of combining molecular docking with molecular dynamics simulations to identify and characterize enzymes capable of catalyzing the reactions required for piperamide synthesis. By addressing both static and dynamic aspects of enzyme-ligand interactions, we have developed a robust framework for enzyme selection and optimization in metabolic pathway design. This methodology holds promise not only for piperamide synthesis but also for the engineering of various other metabolic pathways in the pursuit of sustainable and efficient bioproduction systems.

References